
WSEAS Transactions on Mathematics
Print ISSN: 1109-2769
E-ISSN: 2224-2880
Volume 11, 2012
Issue 1, Volume 11, January 2012
Title of the Paper: Bipartite Theory of Semigraphs
Authors: Y. B. Venkatakrishnan, V. Swaminathan
Abstract: Given a semigraph, we can construct graphs Sa, Sca, Se and S1e. In the same pattern, we construct bipartite graphs CA(S), A(S), VE(S), CA+(S) and A+(S). We find the equality of domination parameters in the bipartite graphs constructed with the domination and total domination parameters of the graphs Sa and Sca. We introduce the domination and independence parameters for the bipartite semigraph. We have defined Xachromatic number, Xa-hyperindependent number and Xa-irredundant number. Using these parameters, we have defined a Xa-dominating sequence chain.
Keywords: Semigraph, Xa-dominating set, Ya-dominating set, Xa-independent set, Xa-hyperindependent set, hyper Xa-independent set
Title of the Paper: Parameter Estimation and Cooperative Effects in Queueing Networks
Authors: Gurami Tsitsiashvili, Marina Osipova
Abstract: This paper is devoted to probability-statistical analysis of Jackson opened and closed networks. A prob- lem of an estimation of product limit distributions parameters using load coefficients of network nodes is solved. Cooperative effects in aggregated opened and closed networks are investigated and optimization procedures of their limit deterministic characteristics are constructed. Formulas of a calculation of limit distributions in superpositions of networks (nodes are replaced by opened networks) are obtained.
Keywords: Phase transition, aggregated networks, superposition of networks, product limit distributions, load coefficients, limit characteristics, parameters estimation
Title of the Paper: Computing Rupture Degrees of Some Graphs
Authors: Fengwei Li, Qingfang Ye, Baohuai Sheng
Abstract: Computer or communication networks are so designed that they do not easily get disrupted under ex- ternal attack and, moreover, these are easily reconstructed when they do get disrupted. These desirable properties of networks can be measured by various parameters such as connectivity, toughness, tenacity and rupture degree. Among these parameters, rupture degree is comparatively better parameter to measure the vulnerability of net- works. In this paper, the authors give the exact values for the rupture degree of the Cartesian product of a path and a cycle. After that, we discuss the rupture degree of total graphs of paths and cycles. Finally, we study the values for rupture degree of powers of paths and cycles.
Keywords: Rupture degree, Vulnerability, Cartesian product, Total graph, Powers of graphs, R-set
Title of the Paper: A New Iterative Method for Equilibrium Problems, Fixed Point Problems of Infinitely Nonexpansive Mappings and a General System of Variational Inequalities
Authors: Jing Zhao, Caiping Yang, Guangxuan Liu
Abstract: In this paper, we introduce a new iterative scheme for finding the common element of the set of common fixed points of infinitely many nonexpansive mappings, the set of solutions of an equilibrium problem and the set of solutions of a general system of variational inequalities for inverse-strongly monotone mappings in Hilbert spaces. We prove that the sequence converges strongly to a common element of the above three sets under some parameters controlling conditions. This main result improve and extend the corresponding results announced by many others. Using this theorem, we obtain three corollaries.
Keywords: Nonexpansive mapping, Equilibrium problem, Fixed point, Inverse-strongly monotone mapping, General system of variational inequality, Iterative algorithm
Title of the Paper: Two New Constructions of Multi-receiver Authentication Codes from Singular Pseudo-Symplectic Geometry over Finite Fields
Authors: Gao You, Chang Liwei
Abstract: In this paper, two new constructions of multi-receiver authentication codes using singular pseudo- symplectic geometry on finite fields are described. Under the assumption that the encoding rules of the transmitter and the receiver are chosen according to a uniform probability distribution, the parameters and the probabilities of success for different types of deceptions are computed by the method of matrix and combinatorial enumeration.
Keywords: Multi-receiver authentication codes, Singular pseudo-symplectic geometry, Finite fields, Construction, Combinatorial enumeration
Title of the Paper: Two Constructions of Multireceiver Authentication Codes from Singular Symplectic Geometry over Finite Fields
Authors: Chen Shangdi, An Lei
Abstract: Multireceiver authentication codes allow one sender to construct an authenticated message for a group of receivers such that each receiver can verify authenticity of the received message. In this paper, two constructions of multireceiver authentication codes from singular symplectic geometry over finite fields are given. The parameters and the probabilities of success for different types of deceptions are computed.
Keywords: Singular symplectic geometry, Multireceiver authentication codes, Finite fields, Construction, Probability
Title of the Paper: Periodic Traveling Wave Solutions for a Coupled Map Lattice
Authors: Mei-Feng Li, Guang Zhang, Hui-Feng Li, Jin-Liang Wang
Abstract: A type of coupled map lattice (CML) is considered in this paper. What we want to do is to define the form of a traveling wave solution and to reveal its existence. Due to the infinite property of the problem, we have tried the periodic case, which can be dealt with on a finite set. The main approach for our study is the implicit existence theorem. The results indicate that if the parameters of the system satisfy some exact conditions, then there exists a periodic traveling wave solution in an exact neighborhood of a given one. However, these conditions are sufficient, but not necessary. In particular, the exact 2-periodic traveling wave solutions are also obtained. It gives some examples for the conditions of parameters, 2-periodic traveling wave solutions exist when these conditions are satisfied.
Keywords: Coupled map lattice, Periodic traveling wave solution, Implicit existence theorem, Nagumo equation, Nontrivial solution
Title of the Paper: Dynamics of Stage-structured Population Models with Harvesting Pulses
Authors: Li Changguo
Abstract: In most models of population dynamics, changes in population due to birth or harvesting are assumed to be time-independent, but many species reproduce or are caught only during a single period of the year. In this paper a single species stage-structured model with density-dependent maturation rate, birth pulse and harvesting pulse is formulated. Using the discrete dynamical system determined by its Poincare map, the existence and stability of nonnegative equilibrium is studied. Furthermore by simulation? a detailed study of the various dynamics are made including period doubling, period halfing, intermittency, crisis, nonunique dynamics and chaotic attractors. The occurrence of these complex dynamic behaviors is related to the fact that minor changes in parameter or initial values can strikingly change the dynamic behaviors of the system. Finally, the dynamic behavior of the system is compared when ì is used as a bifurcation parameter with that when b is used.
Keywords: Stage structure, Density-dependent, Harvesting pulse, Birth pulse, Complexities
Issue 2, Volume 11, February 2012
Title of the Paper: New Hybrid Steepest Descent Algorithms for Variational Inequalities over the Common Fixed Points Set of Infinite Nonexpansive Mappings
Authors: He Songnian, Sun Wenwen
Abstract: New hybrid steepest descent algorithms which are different from Yamada’s hybrid steepest descent algorithms are proposed for solving variational inequalities defined on the common fixed points set of infinite nonexpansive mappings. As the extensions of our main results , algorithms are also given for solving variational inequalities defined on the common fixed points set of infinite ê-strict pseudo-contractions.
Keywords: Hilbert space, fixed point, nonexpansive mapping, strict pseudo-contraction, variational inequality, hybrid steepest descent algorithm
Title of the Paper: Study on the Periodic Solution and Invariant Tori for Iced Cable
Authors: Jing Li, Xiaoli Wei
Abstract: In this paper, the behavior of iced cable with two degrees of freedom is investigated. With Melnikov function of the system, the sufficient condition for the existence of periodic solutions about the system is obtained. The invariant tori of the system is investigated by using transformations and average equation. The conclusion not only enriches the behavior of nonlinear dynamics about iced cable, but also provides the reference to the study of controlling the icing disaster, which is caused by large amplitude low frequency vibration of iced cable.
Keywords: Iced Cable, periodic solution, invariant torus, Melinkov function, transformation
Title of the Paper: Global Solutions for Second Order Impulsive Integro-Differential Equations in Banach Spaces
Authors: Wang Xinfeng, Liu Dalian, Li Chong
Abstract: This paper regards initial value problem for second order impulsive integro-differential equations as some nonlinear vector system. By means of the M¨onch′s fixed point theorem, some existence theorems of solu- tions of the initial value problem are established. The results are newer than all of the previous ones because of the more general form compactness-type condition and the weaker restriction of its coefficients. An example is given to demonstrate our results. Annotation shows that our method can be used to solve the impulsive boundary value problems.
Keywords: Impulsive integro-differential equations, initial value problem, Boundary value problem, Compactness-type condition, Banach space, Fixed point, Operator norm of the matrix
Title of the Paper: Application of an Improved Adaptive Chaos Prediction Model in Aero-Engine Performance Parameters
Authors: Chunxiao Zhang, Junjie Yue
Abstract: Based on the research of complexity and non-linearity of aero-engine exhaust gas temperature (EGT) system, a regularization adaptive chaotic prediction model applied in short time forecasting of EGT was proposed. In this research, we develop a new hybrid particle swarm optimization (HPSO) arithmetic in order to improve the accuracy of the forecasting model. This arithmetic enhanced the ability of dealing with integer variables and constraints by adding and changing some manipulations to fit in with optimizing continuous and integer variables. The test results are based on QAR data supplied by a civil airline company, and show that the proposed framework performs better than the traditional chaotic forecasting model on prediction accuracy. Therefore, this arithmetic is efficient and feasible for a short-term prediction of aero-engine exhaust gas temperature.
Keywords: Exhaust gas temperature (EGT), Regularization, Adaptive chaos prediction, Hybrid particle swarm optimization (HPSO), Principal component regression(PCR), Aero-engine
Title of the Paper: The Singular Diffusion Equation with Boundary Degeneracy
Authors: Qingmei Xie, Huashui Zhan
Abstract: For the heat conduction on a bounded domain with boundary degeneracy, though its diffusion coefficient vanishes on the boundary, it is still possible that the heat flux may transfer across the boundary. A known result shows that the key role is the ratio of the diffusion coefficient near the boundary. If this ratio is large enough, the heat flux transference has not any relation to the boundary condition but is completely controlled by the initial value. This phenomena shows there are some essential differences between the heat flux with boundary degeneracy and that without boundary degeneracy. However, under the assumption on the uniqueness of the weak solutions, the paper obtains that the weak solution of the singular diffusion equation with boundary degeneracy, has the same regular properties as the solution of a singular diffusion equation without boundary degeneracy.
Keywords: Boundary degeneracy, Diffusion equation, Uniqueness, Regular property
Title of the Paper: Some Boundary Properties of Cauchy Type Integral in Terms of Mean Oscillation
Authors: Rahim M. Rzaev, Aysel B. Imanova
Abstract: In this paper radial boundary values of Cauchy type integral are investigated when conditions on integral density are set in terms of mean oscillation of functions. Corresponding statements about boundary values of Poisson integral and conjugate Poisson integral are proved.
Keywords: Cauchy type integral, Poisson integral, boundary values, singular integrals, mean oscillation
Title of the Paper: Introduction to the Angular Functions in Euclidian 2D-space
Authors: Claude Ziad Bayeh
Abstract: The Angular functions are new mathematical functions introduced by the author, they produce rectangular signals, in which period is function of angles and not of time as the previous functions. Similar to trigonometric functions, the angular functions have the same properties as the precedent, but the difference is that a rectangular signal is obtained instead of a sinusoidal signal, and moreover, one can change the width of each positive and negative alternate in the same period. This is not the case of any other trigonometric function. In other hand, one can change the frequency, the amplitude and the width of any period of the signal at any position by using the general form of the angular function. In this paper, an original study is introduced. Thus, the definition of the original part is presented. The angular functions are also defined. These functions are very important in technical subjects. They will be widely used in mathematics and in engineering domains, especially in power electronics, signal theory, propagation of signals and many other topics. Moreover, the Angular functions are the basis of the Elliptical trigonometry and the rectangular trigonometry in which they are new domains introduced in mathematics by the author.
Keywords: Mathematics, geometry, trigonometry, pulse width modulation, signal theory, power electronics
Title of the Paper: Introduction to the General Trigonometry in Euclidian 2D-Space
Authors: Claude Ziad Bayeh
Abstract: The General Trigonometry is a new trend of trigonometry introduced by the author into the mathematical domain. It is introduced to replace the traditional trigonometry; it has huge advantages ahead the traditional one. It gives a general concept view of the trigonometry and forms an infinite number of trigonometry branches and each branch has its own characteristics and features. The concept of the General Trigonometry is completely different from the traditional one in which the study of angles will not be the relation between sides of a right triangle that describes a circle as the previous one, but the idea here is to use the relation between angles and sides of a geometrical form (e.g.: circle, elliptic, rectangle, quadrilateral …) with the internal and external circles formed by the intersection of the geometrical form and the positive parts of x’ox and y’oy axis in the Euclidian 2D space and their projections. This new concept of relations will open a huge gate in the mathematical domain and it can resolve many complicated problems that are difficult or almost impossible to solve with the traditional trigonometry, and it can describe a huge number of multi form periodic signals. The most remarkable trigonometry branches are the “Elliptical trigonometry” and the “Rectangular trigonometry” introduced by the author and published by WSEAS. The importance of these trigonometry branches is that with one function, we can produce multi signal forms by varying some parameters. In this paper, an original study is introduced and developed by the author and some few examples are discussed only to give an idea about the importance of the General Trigonometry and its huge application in all scientific domains especially in Mathematics, Power electronics, Signal theory and processing and in Energy Economic Systems.
Keywords: Modern mathematics, trigonometry, angular function, multi form signal, power electronics
Issue 3, Volume 11, March 2012
Title of the Paper: A Formulation of Conditional States on Steganalysis Approach
Authors: Roshidi Din, Zhamri Che Ani, Azman Samsudin
Abstract: In this paper, we present a consolidated formulation of conditional states from the perspective of steganalysis approach. It has been identified that the conditional states used in steganalysis approach include hypothesis testing, gaussion distribution, hidden markov model and vector analysis space. The main objective of this paper is to find the best approach to fit in using mathematical formulation for steganalytic system based on these conditional states. It is found that there is a boundary of solution between the steganalytic system and analyzed message.
Keywords: Steganalysis, Steganalytic System, Steganography
Title of the Paper: First Order Unstructured Algorithms Applied to the Solution of the Euler Equations in Three-Dimensions
Authors: Edisson Sávio de Góes Maciel
Abstract: In the present work, the Roe, the Steger and Warming, the Van Leer, the Harten, the Frink, Parikh and Pirzadeh, the Liou and Steffen Jr. and the Radespiel and Kroll schemes are implemented, on a finite volume context and using an upwind and unstructured spatial discretization, to solve the Euler equations in the three-dimensional space. The Roe, the Harten, and the Frink, Parikh and Pirzadeh schemes are flux difference splitting ones, whereas the others schemes are flux vector splitting ones. All seven schemes are first order accurate in space. The time integration uses a Runge-Kutta method and is second order accurate. The physical problems of the supersonic flow along a ramp and the “cold gas” hypersonic flow along a diffuser are solved. The results have demonstrated that the Liou and Steffen Jr. scheme is the most conservative algorithm among the studied ones, whereas the Van Leer scheme is the most accurate.
Keywords: Flux difference splitting algorithms, Flux vector splitting algorithms, Unstructured schemes, Euler equations, Three-Dimensions, Supersonic and hypersonic flows
Title of the Paper: The Solutions of Initial Value Problems for Nonlinear Fourth-Order Impulsive Integro-Differential Equations in Banach Spaces
Authors: Zhang Lingling, Yin Jingyi, Liu Junguo
Abstract: In this paper, we investigate the maximal and minimal solutions for initial value problem of fourth order impulsive differential equations by using cone theory and the monotone iterative method to some existence results of solution are obtained. As an application, we give an example to illustrate our results.
Keywords: Banach space, Cone, Initial value problem, Impulsive integro-differential equations
Title of the Paper: Optimal Design of Circular Plates with Internal Supports
Authors: Jaan Lellep, Julia Polikarpus
Abstract: The behaviour of circular plates with internal rigid ring supports is investigated. The material of plates is assumed to be an ideal elastic material obeying the Hooke’s law. The case of an elastic circular plate supported at the edge and resting on an absolutely rigid ring support is studied in a greater detail. Various optimization problems with unknown positions of extra supports are discussed and the problem of optimal location of the internal support is solved under the condition that the cost of the support is proportional to its length. Making use of the variational methods of the optimal control theory necessary conditions of optimality are deduced analytically. Numerical results are presented for the case of uniformly distributed transverse pressure.
Keywords: Plate, internal support, optimization, optimal control
Title of the Paper: Distribution of the Maximum Costs of Products in Direct Selling
Authors: Li-Fei Huang
Abstract: Direct selling companies do not reveal the cost of their products and typically design complex rules for their employees regarding commission. Therefore, determining how much an employee offers to other multilevel above employees is difficult. This study selects one direct selling company to investigate the rules of commission. However, knowing the product costs may assist us in selecting an appropriate choice from among the numerous direct selling companies. Statistical knowledge is used to develop a binomial-geometric model for the complicated commission rules. Using this model, the probability distribution is proved and the mean and standard deviation percentages of cost are found for all employees according to the employee proportions in all stages of the two examples. Employees in lower stages must pay more commission to multilevel above employees, particularly in companies with few top employees. Obtaining sufficient employees to earn commission from the low-cost direct selling product is challenging. Therefore, employees should individually judge whether the direct selling products are worth purchasing and selling.
Keywords: Applied probability, Binomial-geometric distribution, Direct selling, Upgrading and commission rules, Proportion of commission, Distribution of maximum product cost
Title of the Paper: Optimization of Conical Shells of Piece Wise Constant Thickness
Authors: Jaan Lellep, Ella Puman
Abstract: Conical shells with piece wise constant thickness subjected to the distributed transverse pressure and loaded by a rigid central boss are studied. In the paper the both, elastic and inelastic shells are considered. In the case of inelastic shells it is assumed that the material obeys the Hill’s plasticity condition and associated flow rule. The optimization problem is posed in a general form involving as particular cases several different problems. Resorting to the variational methods necessary optimality conditions are derived. The problems regarding to the maximization of the plastic limit load and to the minimum weight design are studied in a greater detail.
Keywords: thin walled shell, optimal design, yield condition, associated flow law, elasticity
Title of the Paper: Positive Solutions of Operator Equations and Nonlinear Beam Equations with a Perturbed Loading Force
Authors: Wen-Xia Wang, Xi-Lan Liu
Abstract: In this paper we are concerned with the existence and uniqueness of positive solutions for an operator equation x = Ax + ëBx on an order Banach space, where A and B are nonlinear operators and ë is a parameter. By properties of cones we obtain that there exists a ë* > 0 such that the operator equation has a unique positive solution which is increasing in ë for ë ? [0, ë*], and further, we give an estimate for ë*. In addition, we discuss the existence and uniqueness of positive solutions for an elastic beam equation with three parameters and one perturbed loading force.
Keywords: Nonlinear operator equation; positive solution; elastic beam equation; perturbed loading force
Title of the Paper: Reentry Flows in Chemical Non-Equilibrium in Three-Dimensions
Authors: Edisson Sávio De Góes Maciel, Amilcar Porto Pimenta
Abstract: This work presents a numerical tool implemented to simulate inviscid and viscous flows employing the reactive gas formulation of thermal equilibrium and chemical non-equilibrium in three-dimensions. The Euler and Navier-Stokes equations, employing a finite volume formulation, on the context of structured and unstructured spatial discretizations, are solved. These variants allow an effective comparison between the two types of spatial discretization aiming verify their potentialities: solution quality, convergence speed, computational cost, etc. The aerospace problem involving the hypersonic flow around a blunt body, in three-dimensions, is simulated. The reactive simulations will involve an air chemical model of five species: N, N_2, NO, O and O_2. Seventeen chemical reactions, involving dissociation and recombination, will be simulated by the proposed model. The Arrhenius formula will be employed to determine the reaction rates and the law of mass action will be used to determine the source terms of each gas species equation.
Keywords: Euler and Navier-Stokes equations, Reactive formulation, Chemical non-equilibrium, Hypersonic flow, Van Leer algorithm, Three-dimensions
Issue 4, Volume 11, April 2012
Title of the Paper: New Families of Eighth-Order Methods with High Efficiency Index for Solving Nonlinear Equations
Authors: Lingling Zhao, Xia Wang, Weihua Guo
Abstract: In this paper, we construct two new families of eighth-order methods for solving simple roots of non- linear equations by using weight function and interpolation methods. Per iteration in the present methods require three evaluations of the function and one evaluation of its first derivative, which implies that the efficiency indexes are 1.682. Kung and Traub conjectured that an iteration method without memory based on n evaluations could achieve optimal convergence order 2n−1. The new families of eighth-order methods agree with the conjecture of Kung-Traub for the case n = 4. Numerical comparisons are made with several other existing methods to show the performance of the presented methods, as shown in the illustration examples.
Keywords: Eighth-order convergence, Nonlinear equations, Weight function methods, Convergence order, Efficiency index
Title of the Paper: On Using the He’s Polynomials for Solving the Nonlinear Coupled Evolution Equations in Mathematical Physics
Authors: E. M. E. Zayed, H. M. Abdel Rahman
Abstract: In this article, we apply the modified variational iteration method for solving the (1+1)- dimensional Ra- mani equations and the (1+1)-dimensional Joulent Moidek (JM) equations together with the initial conditions. The proposed method is modified the variational iteration method by the introducing He’s polynomials in the correction functional. The analytical results are calculated in terms of convergent series with easily computated components.
Keywords: Variational iteration method, Homotopy perturbation methods, Coupled nonlinear evaluation equations, Exact solutions
Title of the Paper: Some Ostrowski Type Inequalities On Time Scales Involving Functions of Two Independent Variables
Authors: Qinghua Feng, Fanwei Meng
Abstract: In this paper, we establish some new Ostrowski type inequalities on time scales involving functions of two independent variables for multiple points, which unify continuous and discrete analysis, and some of which are sharp. The established results extend some known results in the literature, and can be used in the estimate of error bounds for some numerical quadrature formulae.
Keywords: Ostrowski type inequality, Time scales, Numerical integration, Error bound, Sharp bound
Title of the Paper: Existence and Iterative Algorithm of Solutions for a New System of Generalized Set-Valued Mixed Equilibrium-Like Problems in Banach Spaces
Authors: De-Ning Qu, Cao-Zong Cheng
Abstract: A new system of generalized set-valued mixed equilibrium-like problems (in short, S-GMELP) in Ba- nach spaces is discussed. In order to obtain the existence of solutions of S-GMELP, a system of related auxiliary problems (in short, S-AP) is established. On the basis of the existence and uniqueness of solutions of the S-AP, an iterative algorithm for the S-GMELP is constructed. It is proved that the iterative sequence converges some solution of S-GMELP. Finally, an example is given to well exemplify our main result.
Keywords: Equilibrium-like problem, Auxiliary principle technique, Existence, Iterative algorithm, Banach space
Title of the Paper: Convolutional Codes Under Linear Systems Point of View. Analysis of Output-Controllability
Authors: M. I. Garcia-Planas, El M. Souidi, L. E. Um
Abstract: In this work we make a detailed look at the algebraic structure of convolutional codes using techniques of linear systems theory. In particular we study the input-state-output representation of a convolutional code. We examine the output-controllability property and we give conditions for this property. At the end of the paper is presented a brief introduction to the analysis of output controllability for parallel concatenated codes.
Keywords: Codes, linear systems, output-controllability
Title of the Paper: A Study on the Complexity of Multi-Enterprise Output Game in Supply Chain
Authors: Guanhui Wang, Junhai Ma
Abstract: Based on an analysis on a variety of game models in the supply chain, this paper proposes a multi-enterprise output game model under the circumstances of mathematics asymmetry. After a study on Nash equilibrium, the paper analyzes the factors that cause chaos in production decision making among manufacturers and offers numerical simulation. The authors argue that under the circumstances of mathematics asymmetry, the differences in productivity adjustment factor exert great impact on the manufacturers, shown as bifurcation and chaos, whereas the distributors and retailers are scarily affected. The measures to keep the chaos among manufacturers are suggested.
Keywords: supply chain, output game, bifurcation, Lyapunov exponents, discrete dynamical system, complexity
Title of the Paper: The Self-Similar Solutions of a Diffusion Equation
Authors: Huashui Zhan
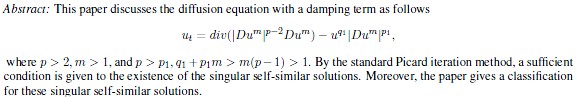
Keywords: Diffusion equation, Damping term, Picard iteration method, Self-similar solution, Singular solution
Issue 5, Volume 11, May 2012
Title of the Paper: 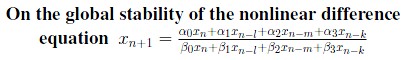
Authors: E. M. E. Zayed, M. A. El-Moneam
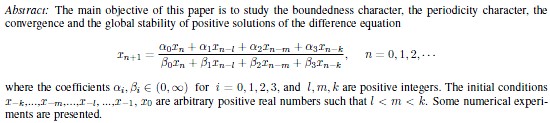
Keywords: Difference equations, boundedness, period two solutions, convergence, global stability
Title of the Paper: An Operator Preserving Inequalities between Polynomials
Authors: Nisar A. Rather, Mushtaq A. Shah
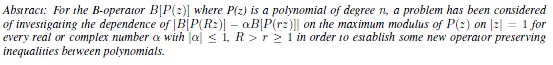
Keywords: Polynomials, B-operator, Inequalities in the complex domain
Title of the Paper: Dynamic Analysis of a System with Warm Standby and Common-Cause Failure
Authors: Weihua Guo, Chun Li, Xia Wang
Abstract: In this paper we analyze the dynamic behavior of a two unit parallel system with warm standby and common-cause failure. By the semigroup theory of linear operators on the Banach space, we give the wellposed- ness of the system and then prove the existence of the nonnegative dynamic solution and the steady solution of system. By spectral analysis of the system operator, we show that all the spectrum points of system operator besides 0 are in the left half-plane, hence we obtain the asymptotic stability of the system. Further we prove that 0 is a dominant eigenvalue of the system. Especially we discuss the essential spectral bound of the system operator and the radius of the essential spectrum of the semigroup associated with the system. Those results show that the dynamic solution of the system converges exponentially to the steady solution. Finally, we analyze the some reliability indic of the system.
Keywords: A two unit parallel system; steady solution; Asymptotic stability; Exponential stability; Reliability
Title of the Paper: Some New Delay Integral Inequalities On Time Scales Arising In The Theory Of Dynamic Equations
Authors: Qinghua Feng, Fanwei Meng
Abstract: In this paper, some new types of delay integral inequalities on time scales are established, which can be used as a handy tool in the investigation of making estimates for bounds of solutions of delay dynamic equations on time scales. Our results generalize the main results in [15, 16, 17], and some of the results in [18, 19].
Keywords: Delay integral inequality; Time scale; Integral equation; Differential equation; Dynamic equation; Bounded
Title of the Paper: On the Routh Reduction of Variational Integrals. Part 1: The Classical Theory
Authors: Ladislav Adamec
Abstract: A geometrical approach to the reductions of one-dimensional first order variational integrals with respect to a Lie symmetry group is discussed. The method includes both the Routh reduction of cyclic variables and the Jacobi-Maupertuis reduction to the constant energy level. In full generality, it may be applied even to the Lagrange variational problems with higher order symmetries.
Keywords: Variational integral, Poincar´e-Cartan form, conservation law, Routh reduction, Jacobi-Maupertuis principle, infinitesimal symmetry, orbit space
Title of the Paper: Classical Theorems for a Gould Type Integral
Authors: Alina Gavrilut, Anca Croitoru
Abstract: In this paper, we continue the study of the Gould type integral introduced in [30] which generalizes the results of [12, 13, 17, 28] and [29]. We obtain various classical properties, such as a mean type theorem, a Lebesgue (Fatou respectively) type theorem, H¨older and Minkowski inequalities etc. Other results concerning measurability, semi-convexity, diffusion and atoms are also established.
Keywords: (multi)(sub)measure, semi-convex, Darboux property, diffused, atom, totally-measurable, Gould integral, Lebesgue theorem, Fatou lemma
Title of the Paper: Riesz Basis and Stability Analysis of the Feedback Controlled Networks of 1-D Wave Equations
Authors: Dongyi Liu, Genqi Xu
Abstract: In this paper, using graph theory and functional analysis approach, we study the Riesz basis property and the stabilization of general networks of 1-D wave equations. Firstly, we derive the vector form of the model under consideration and then discuss the controllers design. We prove that the controlled network is a Riesz system under certain conditions and hence the spectrum determined growth assumption holds. Further we give some necessary and sufficient conditions for the asymptotic stability and the non-stability of the controlled network by spectral conditions. Finally, we apply the obtained results to two networks of special shapes, and analyze their stability by the “irrational dependence”.
Keywords: Wave equation, partial differential network, geometrically continuous type network, Riesz basis, stability
Title of the Paper: Immunopathogenesis in Psoriasis through a Density-Type Mathematical Model
Authors: Biplab Chattopadhyay, Nirmalendu Hui
Abstract: The disease psoriasis occurs as chronic inflammation of skin and appears as scaly red lesions on skin surface. Advent of several immunosuppressive drugs established that the disease stems from immuno-pathogenic disorder in human blood. Cell biological as well as clinical research on the disease reveals that the helper T-cells and other Leucocytes, responsible for human immunity, may lead to psoriasis pathogenesis if produced in plenty at locations close to the dermal region. Research findings also showed that a complex, self-sustaining (cytokine and related) proteins’ network play important role in disease maturation by actually leading to a huge proliferation of epidermal keratinocytes. Disease pathogenesis is identified with such hyperproliferation leading to flaking of skin surface (psoriatic plaques). An excessive generation of nitric oxide by proliferated keratinocytes, through a complex chain of bio-chemical events, is causal to the scaliness of psoriatic plaques. Considering these immunopathogenic mechanisms, we propose and analyse a mathematical time differential model for the disease psoriasis. Outcomes of analysis are consistent with existing cell biological and clinical findings with some new predictions which could be tested further.
Keywords: Psoriasis, Leucocytes, Cytokines, Epidermal Keratinocytes, Immunopathogenesis, Mathematical Model
Issue 6, Volume 11, June 2012
Title of the Paper: On Spatial Analysis of Wind Energy Potential in Malaysia
Authors: Nurulkamal Masseran, Ahmad Mahir Razali, Kamarulzaman Ibrahim, Wan Zawiah Wan Zin, Azami Zaharim
Abstract: Statistical distribution for describing the wind speed at a particular location provides information about the wind energy potential. In this paper, nine different statistical distributions are fitted to the data of average hourly wind speed for 60 wind stations across the west and east Malaysia from the year 2000 to 2009. The distributions found to be most adequate for describing the wind speed at each particular station are determined based on several goodness of fits criteria. The spatial dependence in the data is investigated by making use of the semivariogram involving the expected speed found using the identified distribution for each individual station. Since the spatial dependence in the data of Peninsular Malaysia could not be described well by the semivariogram, the inverse distance weighting method is used for describing the spatial distribution of wind speed. For the data of East Malaysia, however, the power semivariogram is found to be fitted quite well. Accordingly, the kriging method is applied for spatial prediction. It is found that, the regions in the northeast, northwest and southeast of the peninsula have a good potential for wind energy. For East Malaysia, the northeast and southwest regions of Sarawak are found to be the most potential.
Keywords: Wind energy, wind speed distribution, semivariogram, spatial estimation, kriging, inverse distance weighting method
Title of the Paper: Solutions of the Euler and the Laminar and Turbulent Navier-Stokes Equations in Two-Dimensions Using TVD and ENO Algorithms
Authors: Edisson Sávio De Góes Maciel
Abstract: In the present work, the Yee, Warming and Harten and the Yang schemes are implemented, on a finite volume context and using a structured spatial discretization, to solve the Euler and the Navier-Stokes equations in two-dimensions. The former is a TVD high resolution scheme, whereas the latter is an ENO/TVD high resolution algorithm. Both schemes are flux difference splitting ones. An implicit formulation is employed to solve the Euler equations, whereas the Navier-Stokes equations are solved by an explicit formulation. Turbulence is taken into account considering the models of Cebeci and Smith, of Baldwin and Lomax and of Sparlat and Allmaras. The physical problems of the transonic flow along a convergent-divergent nozzle and the supersonic flow along a compression corner are studied in the inviscid case. In the viscous case, the supersonic flow along a ramp is solved. The results have demonstrated that all three algorithms present accurate results.
Keywords: Yee, Warming and Harten algorithm, TVD high resolution scheme, Yang algorithms, ENO/TVD high resolution schemes, Euler and Navier-Stokes equations, Turbulence models
Title of the Paper: Supersonic and Hypersonic Simulations in Three-Dimensions
Authors: Edisson Sávio De Góes Maciel
Abstract: In this work, the numerical schemes of Yee, Warming and Harten, of Yee and Kutler and of Jameson and Mavriplis are implemented, according to a finite volume formulation and structured spatial discretization, to solve the Euler equations in the supersonic
Keywords: Yee, Warming and Harten algorithm, Yee and Kutler algorithm, Jameson and Mavriplis algorithm, Artificial dissipation models, TVD schemes, Euler equations, Three-dimensions.
Title of the Paper: Thermochemical Non-Equilibrium Reentry Flows in Two-Dimensions – Part I
Authors: Edisson Sávio De Góes Maciel, Amilcar Porto Pimenta
Abstract: This work presents a numerical tool implemented to simulate inviscid and viscous flows employing the reactive gas formulation of thermal and chemical non-equilibrium. The Euler and Navier-Stokes equations, employing a finite volume formulation, on the context of structured and unstructured spatial discretizations, are solved. These variants allow an effective comparison between the two types of spatial discretization aiming verify their potentialities: solution quality, convergence speed, computational cost, etc. The aerospace problem involving the hypersonic flow around a blunt body, in two-dimensions, is simulated. The reactive simulations will involve an air chemical model of five species: N, O, N2, O2 and NO. Seventeen chemical reactions, involving dissociation and recombination, will be simulated by the proposed model. The Arrhenius formula will be employed to determine the reaction rates and the law of mass action will be used to determine the source terms of each gas species equation.
Keywords: Thermochemical non-equilibrium, Reentry flow, Five species chemical model, Arrhenius formula, Structured and unstructured solutions, Euler and Navier-Stokes equations, Two-Dimensions.
Title of the Paper: TVD Algorithms Applied to the Solution of the Euler and Navier-Stokes Equations in Three-Dimensions
Authors: Edisson Sávio De Góes Maciel
Abstract: In the present work, the Yee, Warming and Harten, the Harten, the Yee and Kutler, and the Hughson and Beran schemes are implemented, on a finite volume context and using a structured spatial discretization, to solve the Euler and the Navier-Stokes equations in three-dimensions. All four schemes are TVD (“Total Variation Diminishing”) high resolution flux difference splitting ones, second order accurate. An implicit formulation is employed to solve the Euler equations, whereas the Navier-Stokes equations are solved by an explicit formulation. Turbulence is taken into account considering the algebraic models of Cebeci and Smith and of Baldwin and Lomax. The physical problems of the transonic flow along a convergent-divergent nozzle and the supersonic flow along a compression corner in the inviscid case are studied. In the viscous case, the supersonic flow along a ramp is solved. The results have demonstrated that the most severe results are obtained with the Hughson and Beran TVD high resolution scheme, whereas the Yee, Warming and Harten and the Yee and Kutler schemes present more accurate results.
Keywords: Yee, Warming and Harten algorithm, Harten algorithm, Yee and Kutler algorithm, Hughson and Beran algorithm, TVD high resolution schemes, Finite Volumes, Three-dimensions
Title of the Paper: The Progress for Stability of Essential and Critical Spectra of Perturbed C0-semigroups and its Applications to Models of Transport Theory
Authors: Mengmeng Xu, Junguo Jia, Peng Zhao
Abstract: In this paper, we make an analysis for the stable results published recent years about the essential and critical spectra of perturbed C0-semigroups. We also show how these results are applied to models of transport theory. At last we provide and discuss some concerning problems for further study.
Keywords: Perturbed C0-Semigroup, Essential and Critical Spectrum, Transport Theory, Compactness, Norm Continuity, Stability
Title of the Paper: MGD Application to a Blunt Body in Three-Dimensions
Authors: Edisson Sávio De Góes Maciel, Amilcar Porto Pimenta
Abstract: In this paper, the Euler and Navier-Stokes equations are solved, according to the finite volume formulation and symmetrical structured discretization, applied to the problem of a blunt body in three-dimensions. The work of Gaitonde is the reference one to present the fluid dynamics and Maxwell equations of electromagnetism based on a conservative and finite volume formalisms. The MacCormack and the Jameson and Mavriplis symmetrical schemes are applied to solve the conserved equations. Two types of numerical dissipation models are applied, namely: Mavriplis and Azevedo. A spatially variable time step procedure is employed aiming to accelerate the convergence of the numerical schemes to the steady state solution. The results have proved that, when an induced magnetic field is imposed, an increase in the shock standoff distance is observed, which guarantees a minor increase in the temperature at the blunt body nose.
Keywords: Euler and Navier-Stokes equations, Maxwell equations, Magnetogasdynamics formulation, MacCormack algorithm, Jameson and Mavriplis algorithm, Three-dimensions, Finite volumes
Issue 7, Volume 11, July 2012
Title of the Paper: A New Algebraic Solution to Multidimensional Minimax Location Problems with Chebyshev Distance
Authors: Nikolai Krivulin
Abstract: Both unconstrained and constrained minimax single facility location problems are considered in multidimensional space with Chebyshev distance. A new solution approach is proposed within the framework of idempotent algebra to reduce the problems to solving linear vector equations and minimizing functionals defined on some idempotent semimodule. The approach offers a solution in a closed form that actually involves performing matrix-vector multiplications in terms of idempotent algebra for appropriate matrices and vectors. To illustrate the solution procedures, numerical and graphical examples of two-dimensional problems are given.
Keywords: Single facility location problem, Chebyshev distance, Idempotent semifield, Linear equation
Title of the Paper: Study on the Dynamic Model of a Duopoly Game with Delay in Insurance Market
Authors: Wei Xu, Junhai Ma
Abstract: On the basis of domestic and foreign workers’ study, this paper considers the dynamic model of a duopoly price game in insurance market. In the duopoly model, we theoretically analyze the existence and stability of the Nash equilibrium point of the dynamic system, when one player or both players make a delayed decision, then stability conditions are obtained. The numerical simulation results further confirmed the accuracy of the theory. We observe that consideration of the delayed decision cannot change the equilibrium point of the system, but the time to the situation of stabilize will be changed because of the influence of the delayed variable and other parameters. If we increase the value of delayed parameter, the system will take longer time to be stable. If we change the speed of price adjustment and the weight of price of different periods, the time to the situation of stabilize will be changed.
Keywords: Insurance market,duopoly,dynamic game,delayed decision
Title of the Paper: Approximate Solution of Systems of Singular Integro-Differential Equations by Reduction Method in Generalized Holder Spaces
Authors: Feras M. Al Faqih, Nikos E. Mastorakis, Iurie Caraus
Abstract: The computation schemes of reduction method for approximate solution of systems of singular integro- differential equations have been elaborated. The equations are defined on an arbitrary smooth closed contour of complex plane. Estimates of the rate of convergence are obtained in generalized Holder spaces.
Keywords: Reduction Method, Generalized Holder Spaces, systems of singular integro-differential equations
Title of the Paper: Application of a Generalized Bernoulli Sub-ODE Method for Finding Traveling Solutions of Some Nonlinear Equations
Authors: Bin Zheng
Abstract: In this paper, a generalized Bernoulli sub-ODE method is proposed to construct exact traveling solutions of nonlinear evolution equations. We apply the method to establish traveling solutions of the variant Boussinseq equations, (2+1)-dimensional NNV equations and (2+1)-dimensional Boussinesq and Kadomtsev-Petviashvili equations. As a result, some new exact traveling wave solutions are found.
Keywords: Bernoulli sub-ODE method, traveling wave solutions, variant Boussinseq equations, NNV equations, Boussinesq and Kadomtsev-Petviashvili equations
Title of the Paper: A Structured SVD-Like Decomposition
Authors: S. Agoujil, A. H. Bentbib, A. Kanber
Abstract: We present in this paper a method that compute a symplectic SVD-like decomposition for a 2n-by-m rectangular real matrix. This decomposition focus mainly on numerical solution of some linear-quadratic optimal control theory and signal processing problems. In particular the resolution of gyroscopic and linear Hamiltonian systems. Our approach here is based on symplectic reflectors defined on R2n×2. We also give an ortho-symplectic SVD-like decomposition of a 2n-by-2n symplectic real matrix.
Keywords: SVD, Schur Form, Hamiltonian, Skew-Symmetric, Skew-Hamiltonian and Symplectic Matrices, Symplectic Reflector
Title of the Paper: Adomian Decomposition Method to Find the Approximate Solutions for the Fractional PDEs
Authors: Khaled A. Gepreel
Abstract: By introducing the fractional derivatives in the sense of caputo, we use the Adomian decomposition method to construct the approximate solutions for some fractional partial differential equations with time and space fractional derivatives via the time and space fractional derivatives wave equation, the time and space fractional derivatives reduced wave equation and the (1+1)-dimensional Burger’s equation . The result of this problems reveal that the Adomian decomposition method is very powerful, effective, convenient and quite accurate to systems of nonlinear fractional equation.
Keywords: Adomian decomposition method, Fractional calculus, The fractional nonlinear partial differential equations
Title of the Paper: Shape-Preserving Rational Bi-Cubic Spline for Monotone Surface Data
Authors: Muhammad Abbas, Ahmad Abd Majid, Mohd Nain Hj Awang, Jamaludin Md Ali
Abstract: In this paper, we extended the rational cubic function to rational bi-cubic function that presents a smooth, visually pleasant and interactive view of monotonicity preserving surface. Moreover, it involves six free parameters in its description. These free parameters are arranged in such a way where two of these are constrained to preserve the monotonicity, while the remaining other four free parameters are left free to designer for the refinement of monotone surface as desired. The scheme under discussion is 1C, flexible, simple, local and economical as compared to existing schemes. Numerical examples are provided to demonstrate that the anticipated scheme is interactive and smooth.
Keywords: Shape preserving interpolation, Rational cubic function, Rational Bi-cubic function, Monotone surface, Monotone surface data, Free parameters
Issue 8, Volume 11, August 2012
Title of the Paper: A Filled Function Algorithm for Multiobjective Optimization
Authors: Liuyang Yuan, Zhongping Wan, Jiawei Chen
Abstract: In this paper a filled function algorithm is applied to compute one of the nonisolated Pareto optimal points of an unconstrained multiobjective optimization problem. Firstly, the original problem is converted into an equivalent global optimization problem. Subsequently, a novel filled function algorithm is presented for solving the corresponding global optimization problem. The implementation of the algorithm on several test problems is reported with numerical results.
Keywords: Multiobjective optimization, Filled function method, Global optimization, Local minimizer, Global minimizer, Pareto optimal
Title of the Paper: Multiple Multidimensional Sequence Alignment Using Generalized Dynamic Time Warping
Authors: Parinya Sanguansat
Abstract: Nowadays, the alignment of multidimensional sequences is required in many applications especially for multimedia data. The ordinary DTW is not well satisfied this condition because it can only align a pair of 1D sequences at once. Applying traditional DTW to these tasks not only makes each pairwise alignments are independent but also causes each dimensions are compared separately. In this paper, the generalized algorithm of Dynamic Time Warping (DTW) is proposed for multiple multidimensional time series alignments, called Multiple Multidimensional Dynamic Time Warping (MM-DTW). This algorithm utilizes all dimensions to obtain the optimal path and aligns multiple signals simultaneously. After alignment, the regular similarity measurement can be used to these aligned signals. The performances of MM-DTW are investigated by the nearest neighbor classifier compared to the ordinary DTW and its multidimensional modified algorithm. Experiments on real-world application, Query by humming, demonstrate the improved performance of the proposed method over the other algorithms.
Keywords: Multiple multidimensional dynamic time warping, Dynamic time warping, Multidimensional sequences, Dynamic programming, Signal processing, Query by humming
Title of the Paper: The Nonexistence of the Solution for Quasilinear Parabolic Equation Related to the P-Laplacian
Authors: Huasui Zhan

Keywords: Quasilinear parabolic equation, Cauchy problem, Nonexistence, Dirac measure
Title of the Paper: Positive Periodic Solutions for an Impulsive Neutral Delay Model of Single-Species Population Growth on Time Scales
Authors: Meng Hu, Lili Wang
Abstract: By using a fixed point theorem of strict-set-contraction, some criteria are established for the existence of positive periodic solutions for an impulsive neutral delay model of single-species population growth on time scales. Finally, an example is given to illustrate the main results.
Keywords: Positive periodic solution; Neutral delay model; Impulse; Strict-set-contraction; Time scale
Title of the Paper: Chaos Control and Synchronization of a Fractional-Order Autonomous System
Authors: Wang Hongwu, Ma Junhai
Abstract: Liu, Liu, and Liu, in the paper “A novel three-dimensional autonomous chaos system, Chaos, Solitons and Fractals. 39 (2009) 1950-1958”, introduce a novel three-dimensional autonomous chaotic system. In this paper, the fractional-order case is considered. The lowest order for the system to remain chaotic is found via numerical simulation. Stability analysis of the fractional-order system is studied using the fractional Routh-Hurwitz criteria. Furthermore, the fractional Routh-Hurwitz conditions are used to control chaos in the proposed fractional-order system to its equilibria. Based on the fractional Routh-Hurwitz conditions and using specific choice of linear controllers, it is shown that the fractionalorder autonomous system can be controlled to its equilibrium points. In addition, the synchronization of the fractional-order system and the fractional-order Liu system is studied using active control technique. Numerical results show the effectiveness of the theoretical analysis.
Keywords: Fractional-order Chaos Predictor-correctors scheme The fractional Routh-Hurwitz criteria Feedback control Synchronization Active control
Title of the Paper: Solving the Face Recognition Problem using QR Factorization
Authors: Jianqiang Gao, Liya Fan, Lizhong Xu
Abstract: Inspired and motivated by the idea of LDA/QR presented by Ye and Li, in addition, by the idea of WK- DA/QR and WKDA/SVD presented by Gao and Fan. In this paper, we first consider computational complexity and efficacious of algorithm present a PCA/range(Sb) algorithm for dimensionality reduction of data, which transforms firstly the original space by using a basis of range(Sb) and then in the transformed space applies PCA. Considering computationally expensive and time complexity, we further present an improved version of PCA/range(Sb), denot- ed by PCA/range(Sb)-QR, in which QR decomposition is used at the last step of PCA/range(Sb). In addition, we also improve LDA/GSVD, LDA/range(Sb) and PCA by means of QR decomposition. Extensive experiments on face images from UCI data sets show the effectiveness of the proposed algorithms.(Sb
Keywords: QR decomposition, PCA/range(Sb)-QR, PCA/GSVD-QR, LDA/range(Sb)-QR, PCA/QR, Algorithm
Title of the Paper: On the Trivariate Polynomial Interpolation
Authors: Suleyman Safak
Abstract: This paper is concerned with the formulae for computing the coefficients of the trivariate polynomial interpolation (TPI) passing through (m+1)(n+1)(r+1) distinct points in the solid rectangular region. The TPI is formulated as a matrix equation using Kronecker product and Khatri-Rao product of the matrices and the coefficients of the TPI are computed using the generalized inverse of a matrix. In addition, the closed formulae of the coefficients of the bivariate and univariate polynomial interpolations are obtained by the use of the inverse of the Vandermonde matrix. It is seen that the trivariate polynomial interpolation can be investigated as the matrix equation and the coefficients of the TPI can be computed directly from the solution of the matrix equation. Also, it is shown that the bivariate polynomial interpolation (BPI) is the special case of the TPI when0=r. Numerical examples are represented.
Keywords: Polynomial interpolation, trivariate polynomial, bivariate polynomial, matrix equation/font>
Issue 9, Volume 11, September 2012
Title of the Paper: Mean Square Stability of Periodic Solution for Stochastic Cohen-Grossberg-Type BAM Neural Networks with Delays
Authors: Chunfang Miao, Yunquan Ke
Abstract: In this paper, the mean square exponential stability of the periodic solution of stochastic Cohen- Grossberg-Type BAM neural networks with delays are investigated. By constructing suitable Lyapunov function, applying Itˆo formula, integral mean-value theorem and Poincar´e mapping, we give several sufficient conditions to guarantee the mean square exponential stability of the periodic solution of the system. An illustrative example is also given in the end to show the effectiveness of our results.
Keywords: Stochastic Cohen-Grossberg-type BAM neural networks; Itˆo formula; Poincar´e mapping; periodic solution; mean square exponential stability
Title of the Paper: Improvement of Ranking Method Based on Effectiveness of Units in Society by Common Weights Approach in DEA
Authors: Ali Payan, Abbasali Noura, Mehrdad Nozohour
Abstract: The aim of this paper is to modify the suggested method by Noura et al. [25], which is a ranking method based on the effectiveness of each unit in society. They utilized the assigned weights by manager for ranking decision making units (DMUs) on the basis of the effectiveness in society, however, this is not a conventional method for determining the weights. This paper proposes common weights approach for improving its method. A multi-objective linear fractional is derived and then it was converted to a multi-objective linear programming by Taylor series. The model is solved by Max Min method. Based on the obtained optimal solution, common weights are acquired and then DMUs will be ranked. The proposed method is illustrated by ranking Taiwan forests after reorganization.
Keywords: Data envelopment analysis, Super efficiency, Effectiveness, Multi-objective linear fractional programming, Common weights, Taylor series
Title of the Paper: Effect of Variable Viscosity on Convective Heat and Mass Transfer by Natural Convection from Vertical Surface in Porous Medium
Authors: M. B. K. Moorthy, K. Senthilvadivu
Abstract: The aim of this paper is to investigate the effect of variable viscosity on free convective heat and mass transfer from a vertical plate embedded in a saturated porous medium. The governing equations of continuity, momentum, energy and concentration are transformed into non linear ordinary differential equations using similarity transformations and then solved by using Runge – Kutta – Gill method along with shooting technique. Governing parameters for the problem under study are the variable viscosity, the buoyancy ratio and the Lewis number. The velocity, temperature and concentration distributions are presented and discussed. The Nusselt and Sherwood number are also derived. The numerical values of local Nusselt and local Sherwood numbers have also been computed for a wide range of governing parameters. The viscous and thermal boundary layer thicknesses are discussed
Keywords: Free convection, Heat transfer, Mass transfer, Variable viscosity, Porous medium
Title of the Paper: Some Results on Tenacity of Graphs
Authors: Fengwei Li

Keywords: Tenacity, Vulnerability, Cartesian product, Gear graph, Powers of graphs, T-set
Title of the Paper: An Efficient Approach for the Optimization version of Maximum Weighted Clique Problem
Authors: S. Balaji, N. Revathi
Abstract: Given a graph and a weight function defined on the vertex set of a graph, the maximum weighted clique (MWC) problem calls for finding the number of vertices with maximum total weight and also any two of vertices are pairwise adjacent. In this paper, an edge based local search algorithm, called ELS, is proposed for the MWC, a well-known combinatorial optimization problem. ELS is a two phased local search method effectively finds the near optimal solutions for the MWC. A parameter ‘support’ of vertices defined in the ELS greatly reduces the more number of random selections among vertices and also the number of iterations and running times. Computational results on DIMACS benchmark graphs indicate that ELS is capable of achieving state-of-the-art-performance for the maximum weighted clique with reasonable average running times.
Keywords: Maximum weighted clique, local search, heuristic, NP-complete
Title of the Paper: Introduction to the Elliptical Trigonometry in Euclidian 2D-space with Simulation of Four Elliptical Trigonometric Functions Jes, Jes-x, Mar and Rit
Authors: Claude Ziad Bayeh
Abstract: Trigonometry is a branch of mathematics that deals with relations between sides and angles of triangles. The trigonometric functions are very important in technical subjects like Astronomy, Relativity, science, engineering, architecture, and even medicine. In this paper, the elliptical trigonometry is introduced in order to be in the future a part of the General Trigonometry topic. The concept of the Elliptical Trigonometry is completely different from the traditional trigonometry in which the study of angles is not the relation between sides of a right triangle that describes a circle as the previous one, but the idea here is to use the relation between angles and sides of an ellipse form with the internal and external circles formed by the intersection of the ellipse form and the positive parts of x’ox and y’oy axis in the Euclidian 2D space and their projections. This new concept of relations will open a huge gate in the mathematical domain and it can resolve many complicated problems that are difficult or almost impossible to solve with the traditional trigonometry, and it can describe a huge number of multi form periodic signals.
Keywords: Mathematics, geometry, trigonometry, angular function, multi form signal, power electronics
Title of the Paper: Existence of Positive Solutions to a Four-Point Boundary Value Problems
Authors: Dehong Ji, Weigao Ge

Keywords: Positive solutions; p−Laplacian; Boundary value problem; Monotone iterative technique; Completely continuous; Cone
Title of the Paper: Angular Coordinate System in Euclidian 2D Space
Authors: Claude Ziad Bayeh
Abstract: The Angular Coordinate System is a new and original mathematical Coordinate System introduced by the author in the mathematical domain. It has own properties similar to other coordinate systems such as Cylindrical coordinate system, Cartesian coordinate system or any other coordinate system. The main goal of introducing this coordinate system is to describe the whole universe in 2D space using two angles only formed by the center of a unit circle of the universe. This new coordinate system is introduced also to facilitate the drawing of many complicated curves that are difficult to produce using the traditional coordinate systems. It has many applications in physics for example the unit circle can be considered as a black hole and we have to describe the formed universe according to this black hole using only two angles. In this paper a complete study is introduced for the new coordinate system and few examples are presented in order to give an idea about how to form and study curves in the Angular coordinate system.
Keywords: Angular coordinate system, two angles, unit circle, black hole, Cartesian coordinate system, mathematics
Title of the Paper: Some New Results Related To A Generalized Ostrowski-Gruss Type Inequality On Time Scales
Authors: Bin Zheng
Abstract: In this paper, we present some new bounds for a generalized Ostrowski-Gr¨uss type integral inequality on time scales, which on one hand unify continuous and discrete analysis, on the other hand extend some known results in the literature. Some of the bounds for the presented Ostrowski-Gr¨uss type inequality are sharp.
Keywords: Ostrowski type inequality; Gr¨uss type inequality; Time scales; Bounds; Numerical integration; Error estimate
Title of the Paper: High Accuracy and Multiscale Multigrid Computation for Three Dimensional Biharmonic Equations
Authors: Hoda Ibrahim
Abstract: The multiscale multigrid method is presented in this article to solve the linear systems arising from a fourth order discretisation. We used a symbolic algebra package Mathematica to derive a family of finite difference approximations on a 27 point compact stencil. The unknown solution and its second derivatives are carried as unknowns at selected grid points. A set of test problems are presented to demonstrate the efficiency and accuracy of the fourth order compact scheme.
Keywords: Boundary value problems; three-dimensional biharmonic equation; fourth order compact scheme; multiscale multigrid method
Issue 10, Volume 11, October 2012
Title of the Paper: New Asymptotic and Algorithmic Results in Calculation of Random Graphs Connectivity
Authors: Gurami Tsitsiashvili, Marina Osipova
Abstract: This paper is devoted to calculations of connectivity probabilities and distributions of connectivity com- ponents numbers in planar and recursively defined and parallel-sequential random graphs. These calculations are based on asymptotic formulas for connectivity probabilities and on recurrent relations for different deterministic and stochastic characteristics of random graphs and on limit theorems for Markov chains with finite state set. Main aim of these paper is to decrease calculational complexity of considered problems solutions.
Keywords: Planar graph, cross section, connectivity probability, recursive definition, calculational complexity, central limit theorem, law of large numbers
Title of the Paper: Applying Fuzzy AHP Approach to Evaluate Key Operational Safety Elements for Exclusive Container Terminals of Kaohsiung Port in Taiwan
Authors: Ji-Feng Ding, Wen-Jui Tseng
Abstract: There are many accidents and risks occurred in many activities of operational systems at exclusive container terminals (ECTs) of Kaohsiung port in Taiwan. The container operators nowadays are facing great competitions on how reducing risks to manage those operational systems and activities at Kaohsiung port. Hence, the main purpose of this paper is to apply the fuzzy analytic hierarchy process (AHP) approach to empirically study the risk identification on key operational safety elements (OSEs) for ECTs of Kaohsiung port in Taiwan. To facilitate the main issue for obtaining the preliminary OSEs, the four dimensions and sixteen initially important elements are derived from academic literature and interviewed with senior managers working at ECTs of Kaohsiung port. Subsequently, the proposed fuzzy AHP approach is used to measure relative weights for assessing those safety elements. Finally, the systematic appraisal approach is to perform the empirical survey via AHP questionnaires. The results of this study show that: (1) the aspect of most important risk is the man dimension; and (2) the top six critical OSEs are ‘operators’ mistakes and faults on operations,’ ‘communication misunderstanding,’ ‘execution of the job safety rules and regulations,’ ‘human carelessness and omissions,’ ‘carrying out the standard operating procedures (SOPs),’ and ‘not selecting inherently safety protection of machines and equipment,’ respectively. The finding of the empirical results showed that the top four risk factors all belonged to the man dimension. The safety and risk issues indicate that human error is associated with the majority of risk. It is suggested that the risk strategies on the man dimension can be focused on this aspect of safety operations of ECTs at Kaohsiung port.
Keywords: Risk; Safety; Container terminal; Fuzzy analytic hierarchy process (AHP)
Title of the Paper: Hyper Domination in Bipartite Semigraphs
Authors: Y. B. Venkatakrishnan, V. Swaminathan

Keywords: Semigraphs, Bipartite semigraphs, hyper dominating set, hyper independent set, hyper irredundant set
Title of the Paper: Introduction to the Rhombus Trigonometry in Euclidian 2D-space with simulation of four Rhombus trigonometric functions RhJes, RhJes-x, RhMar and RhRit
Authors: Claude Ziad Bayeh
Abstract: The Rhombus Trigonometry is an original study introduced in the mathematical domain by the author. Trigonometry is a branch of mathematics that deals with relations between sides and angles of triangles. It has some relationships to geometry, though there is disagreement on exactly what is that relationship. For some scientists, trigonometry is just a subtopic of geometry. The trigonometric functions are very important in technical subjects like Astronomy, Relativity, Science, Engineering, Architecture, and even Medicine. In this paper, the Rhombus trigonometry is introduced in order to be a part of the General Trigonometry topic. Thus, the definition of this original part is presented, and the Rhombus trigonometric functions are also defined. The importance of these functions is by producing multi signal forms by varying some parameters of a single function. Different signals and forms are analyzed and discussed. The concept of the Rhombus Trigonometry is completely different from the traditional trigonometry in which the study of angles is not the relation between sides of a right triangle that describes a circle as the previous one, but the idea here is to use the relation between angles and sides of a rhombus form with the internal and external circles formed by the intersection of the rhombus form and the positive parts of x’ox and y’oy axis in the Euclidian 2D space and their projections. This new concept of relations will open a huge gate in the mathematical domain and it can resolve many complicated problems that are difficult or almost impossible to solve with the traditional trigonometry, and it can describe a huge number of multi-form periodic signals.
Keywords: Mathematics, geometry, trigonometry, angular function, multi form signal, power electronics.
Title of the Paper: Oscillation Criteria for a Class of Third Order Dynamic Equation with Damping on Time Scales
Authors: Qinghua Feng, Fanwei Meng
Abstract: In this paper, some new oscillation criteria for a class of third order dynamic equations with damping on time scales are established by a generalized Riccati transformation technique. The established oscillation criteria unify continuous and discrete analysis, and are new results so far in the literature.
Keywords: Oscillation; Dynamic equations; Qualititative properties; Time scales; Third order; Damping
Title of the Paper: On an Extension of Camina′s Theorem on Conjugacy Class Sizes
Authors: Qingjun Kong
Abstract: Let G be a finite group. We extend Alan Camina′s theorem on conjugacy class sizes which asserts that if the conjugacy class sizes of G are exactly {1; pa; qb; paqb}, where p and q are two distinct primes and a and b are integers, then G is nilpotent.
Keywords: Conjugacy class sizes; Nilpotent groups; Solvable groups; Sylow p-subgroup; Finite groups
Title of the Paper: New Approach to Find the Exact Solution of Fractional Partial Differential Equation
Authors: Abdolamir Karbalaie, Mohammad Mehdi Montazer, Hamed Hamid Muhammed
Abstract: In this study, we present the exact solution of certain fractional partial differential equations (FPDE) by using a modified homotopy perturbation method (MHPM).The exact solutions are constructed by choosing an appropriate initial approximation and only one term of the series obtained by MHPM. The exact solutions for initial value problems of FPDE are analytically derived. The methods introduced an efficient tool for solving a wide class of time-fractional partial differential equations.
Keywords: Mitting-leffler functions, Green function, Caputo derivative, Backward Klomogorov equation
Title of the Paper: Transient Temperature Solutions of a Cylindrical Fin with Lateral Heat Loss
Authors: P.-Y. Wang, G.-C. Kuo, Y.-H. Hu, W.-L. Liaw, K.-J Wang, K.-Y Kung
Abstract: Analytical temperature solutions to the transient heat conduction for a two dimensional cylindrical fin with lateral heat source together with various convective effects on lateral surface is obtained by the method of superposition and separation variables. The temperature distributions are generalized for a linear combination of the product of Bessel function, Fourier series and exponential type for nine different cases. Relevant connections with some other closely-related recent works are also indicated.
Keywords: Bessel function, Fourier series, Heat conduction, Temperature distribution, Separation variables, Superposition.
Title of the Paper: Positive Solutions of BVPs for Some Second-Order Four-Point Difference Systems
Authors: Yitao Yang, Fanwei Meng
Abstract: This paper is concerned with one type of boundary value problems (BVPs). We first construct Green functions for a second-order four-point difference equation, and try to find delicate conditions for the existence of positive solutions. Our main tool is a nonlinear alternative of Leray-Schauder type, krasnosel’skii’s fixed point theorem in a cone and Leggett-Williams fixed point theorem.
Keywords: Discrete system; Positive solutions; Cone; Nonlinear alternative; Leggett-Williams fixed point theorem; Fixed point
Title of the Paper: Orthogonal Least Trimmed Absolute Deviation Estimator for Multiple Linear Errors-in-Variables Model
Authors: Huirong Cao, Fuchang Wang
Abstract: Orthogonal least trimmed absolute deviation (OLTAD) estimator of the multiple linear errors-in-variables (EIV) model is presented. We show that the OLTAD estimator has the high breakdown point and appropriate prop- erties. A new decimal-integer-coded genetic algorithm(DICGA) and Fast-OLTAD method for solving OLTAD estimators are also proposed. Computational experiments of the OLTAD estimator of the multiple linear EIV model on benchmark data and synthetic data are provided. The results indicate that the DICGA and Fast-OLTAD methods perform well in dealing with high leverage outliers in reasonable computational time.
Keywords: Linear errors-in-variables model, Robust estimator, Orthogonal least trimmed absolute deviation estimator, Decimal-integer-coded genetic algorithm, Fast-OLTAD method, Outliers
Issue 11, Volume 11, November 2012
Title of the Paper: Finite Group with c-Normal or s-Quasinormally Embedded Subgroups
Authors: Ping Kang

Keywords: C-normal subgroup; s-quasinormally embedded subgroup; supersolvable groups; Sylow p-subgroup; Finite groups
Title of the Paper: Analysis of Behavior of the Eigenvalues and Eigenvectors of Singular Linear Systems
Authors: M. I. Garcia-Planas, S. Tarragona
Abstract: Let E(p)x_ = A(p)x + B(p)u be a family of singular linear systems smoothly dependent on a vector of real parameters p = (p1, . . . , pn). In this work we construct versal deformations of the given differentiable family under an equivalence relation, providing a special parametrization of space of systems, which can be effectively applied to perturbation analysis. Furthermore in particular, we study the behavior of a simple eigenvalue of a singular linear system family E(p)x_ = A(p)x + B(p)u.
Keywords: Singular linear systems, Eigenvalues, Perturbation, Versal deformation
Title of the Paper: Some New Generalized Volterra-Fredholm Type Nonlinear Discrete Inequalities
Authors: Bin Zheng
Abstract: In this paper, we establish some new generalized Volterra-Fredholm type nonlinear discrete inequalities, based on which we study the boundedness of the solutions of a kind of Volterra-Fredholm type sum-difference equation. As a result, New bounds to the solutions are established under some suitable conditions. The established inequalities are further generalizations of the results by Zheng [Adv. Differ. Equ. Article ID: 30 (2011) 1-16 ], Ma [J. Comput. Appl. Math. 233 (2010) 2170-2180], and Zheng [Abstr. Appl. Anal. Article ID: 584951 (2011) 1-24].
Keywords: Nonlinear inequalities; Discrete inequalities; Volterra-Fredholm type inequalities; Gronwall-Bellman type inequalities; Finite difference equations; Boundedness
Title of the Paper: Thermochemical Non-Equilibrium Reentry Flows in Two-Dimensions – Part II
Authors: Edisson Sávio De Góes Maciel, Amilcar Porto Pimenta
Abstract: This work presents a numerical tool implemented to simulate inviscid and viscous flows employing the reactive gas formulation of thermochemical non-equilibrium. The Euler and Navier-Stokes equations, employing a finite volume formulation, on the context of structured and unstructured spatial discretizations, are solved. These variants allow an effective comparison between the two types of spatial discretization aiming verify their potentialities: solution quality, convergence speed, computational cost, etc. The aerospace problems of the hypersonic flow around a double ellipse and around a reentry capsule, in two-dimensions, are simulated. The reactive simulations will involve an air chemical model of five species: N, O, N2, O2 and NO. Seventeen chemical reactions, involving dissociation and recombination, will be studied. The Arrhenius formula will be employed to determine the reaction rates and the law of mass action will be used to determine the source terms of each gas species equation.
Keywords: Euler and Navier-Stokes equations, Reactive formulation, Thermochemical non-equilibrium, Hypersonic flow, Van Leer algorithm, Finite Volumes, Unstructured discretization
Title of the Paper: A Non-Monotone Tensor Method for Unconstrained Optimization Problems
Authors: Xianjun Shi, Lei Yang, Ying Zhang
Abstract: The tensor method for unconstrained optimization was first introduced by Schnable and Chow [SIAM Journal on Optimization, 1 (1991): 293–315], where each iteration bases upon a fourth order model for the objec- tive function. In this paper, we propose a tensor method with a non-monotone line search scheme for solving the unconstrained optimization problem, and show the convergence of the method. We evaluate the proposed method by several numerical examples, and compare the obtained numerical results with those by the modified Newton method, the tensor method, and the monotone tensor method. Through the numerical results, we can see that the new method is more effective than others for the problems we tested.
Keywords: Unconstrained optimization, non-monotone linear search, non-monotone tensor method
Title of the Paper: Dynamic Study of Mathematical Models on Antibiotics and Immunologic Adjuvant Against Toxoplasmosis
Authors: Yongzhen Pei Ye Liu, Changguo Li
Abstract: In this paper, three mathematical models concerning the effect of leucocyte, antibiotics and immunologic adjuvant against toxoplasma gondii were proposed respectively. In the case in which toxoplasmosis was inhibited by leucocyte in the host, it is shown that toxoplasmosis can be destroyed depending on the immune strength of the host. In the case in which antibiotics treatment is used, it is observed that input concentration of antibiotics has significant influence on toxoplasmosis. In the case in which immunologic adjuvant was imported to the body of the host, it can improve immunity of the parasitifer to attain the propose of killing toxoplasma gondii eventually.
Keywords: Toxoplasmosis, leucocyte, antibiotics, immunologic adjuvant, uniformly persistence
Title of the Paper: On Vulnerability of Power and Total Graphs
Authors: Qingfang Ye
Abstract: In communication networks, greater degrees of stability or less vulnerability is required. The vulnera- bility of communication network measures the resistance of the network to the disruption of operation after the failure of certain stations or communication links. If the network begins losing communication links or processors, then there is a loss in its effectiveness. Thus, communication networks must be so designed that they do not easily get disrupted under external attack and, moreover, these are easily reconstructible if they do get disrupted. These desirable properties of networks can be measured by various graph parameters like toughness, integrity, scattering number, tenacity and rupture degree. Power graphs and total graphs constitute a large class of graphs and which are widely used in systems ranging from large supercomputers to small embedded systems-on-a-chip. In this paper, we firstly give the exact values for the integrity and toughness of powers of paths. After that, the vulnerability parameters such as integrity, toughness, rupture degree of total graphs of some special graphs are calculated. Fi- nally, the relationships between some vulnerability parameters, namely the integrity, toughness, scattering number, tenacity and rupture degree are established.
Keywords: Vulnerability, Integrity, Toughness, Scattering number, Tenacity, Rupture degree, Total graph, Power graph
Title of the Paper: An Extended (G′/G)− Expansion Method and its Applications to the (2+1)-Dimensional Nonlinear Evolution Equations
Authors: Elsayed M. E. Zayed, Mahmoud A. M. Abdelaziz
Abstract: By using an extended (G?/G)-expansion method, we construct the traveling wave solutions of the (2+1)- dimensional Painleve integrable Burgers equations, the (2+1)-dimensional Nizhnik-Novikov-Veselov equations, the (2+1)-dimensional Boiti-Leon-Pempinelli equations and the (2+1)-dimensional dispersive long wave equa- tions, where G satisfies the second order linear ordinary differential equation. By using this method, new exact solutions involving parameters, expressed by hyperbolic and trigonometric function solutions are obtained. When the parameters are taken as special values, some solitary wave solutions are derived from the hyperbolic function solutions.
Keywords: Extended (G′/G)-expansion method; Traveling wave solutions; Painleve integrable Burgers equations; Nizhnik-Novikov-Veselov equations; Boiti-Leon-Pempinelli equations; Dispersive long wave equations; Solitary solutions
Title of the Paper: Multistability of Competitive Neural Networks with Time-Delay in the Saturation Region
Authors: Yunquan Ke, Chunfang Miao
Abstract: In this paper, the multistability analysis of the competitive neural networks with time-delay are investigated based on the stability theory, by selecting properly the system parameters, using solution matrix property and inequality technique, several novel sufficient conditions ensuring the existence and exponential stability of equilibria are obtained when the equilibrium point located in the saturation region. These conditions can be directly derived from the synaptic weights, the strength of the external stimulus and the external input of the competitive neural networks, and be verified easily. In addition, four examples are given to show the effectiveness of the results.
Keywords: Competitive neural networks; saturation regions; multistability; exponential stable
Issue 12, Volume 11, December 2012
Title of the Paper: Exponential Stability of Reaction-Diffusion Cohen-Grossberg-Type BAM Neural Networks with Time Delays
Authors: Fengyan Zhou
Abstract: The global exponential stability is investigated for a class of reaction-diffusion Cohen-Grossberg-type BAM neural networks with time delays. By constructing suitable Lyapunov functional and using homeomorphism mapping, several sufficient conditions guaranteeing the existence, uniqueness and global exponential stability of reaction-diffusion Cohen-Grossberg-type BAM neural networks with time delays are given. Moreover, two illus- trative examples are presented to illustrate the feasibility and effectiveness of our results.
Keywords: Reaction-diffusion Cohen-Grossberg-type BAM neural networks; Time delays; Lyapunov functional; Equilibrium point; Exponential stability
Title of the Paper: Modeling Cyprus Stock Market
Authors: Athina Bougioukou
Abstract: The intention of this research is to understand the behavior of the Cyprus Stock Market. Two time series are used as representatives: the FTSE/CySE 20 and the General index. Both return series are characterized by the presence of heavy tails and reject the Gaussian models. We use a-stable distributions to model the data. Although statistical tests accept the null hypothesis empirical findings of FTSE/CySE 20 show that return distribution takes the shape of a Gaussian distribution at 345 days and the tails appear to become less heavy for less frequent series. Self-similarity is also explored and Hurst exponent is H ? (0:6; 0:65), showing persistent return time series.
Keywords: a-stable distribution, Hurst exponent, heavy tails, infinite variance, Anderson-Darling, Kolmogorov-Smirnov criteria
Title of the Paper: Traveling Wave Solutions For Two Nonlinear Lattice Equations By An Extended Riccati Sub-equation Method
Authors: Chuanbao Wen
Abstract: In this paper, we apply an extended Riccati sub-equation method to establish new exact solutions for two nonlinear lattice equations. As a result, new traveling wave solutions including hyperbolic function solutions, trigonometric function solutions and rational function solutions are obtained, and some of them are generalizations of some known results in the literature obtained by the (G?/G)-expansion method.
Keywords: Nonlinear lattice equations; Riccati sub-equation method; Exact solutions; Traveling wave solutions; Differential-difference equations; Nonlinear evolution equations
Title of the Paper: Normal Structure, Slices and Other Properties in Banach Spaces
Authors: Satit Saejung, Ji Gao

Keywords: Fixed point, modulus of NUC, modulus of UKK*, normal structure, Slices, super-reflexive, and ultra-product space.
Title of the Paper: Two Constructions of Multi-Sender Authentication Codes with Arbitration based Linear Codes
Authors: Chen Shangdi, Chang Lizhen
Abstract: Multi-sender authentication codes allow a group of senders to construct an authenticated message for a receiver such that the receiver can verify authenticity of the received message. In this paper, we construct two multi-sender authentication codes with arbitration from Linear codes. The parameters and the probabilities of deceptions are also calculated.
Keywords: Multi-sender, Authentication code, Arbitration, Linear code, Finite field
Title of the Paper: Krylov Subspace Type Methods for Solving Projected Generalized Continuous-Time Lyapunov Equations
Authors: Yujian Zhou, Yiqin Lin, Liang Bao
Abstract: In this paper we consider the numerical solution of projected generalized continuous-time Lyapunov equations with low-rank right-hand sides. The interest in this problem stems from stability analysis and control problems for descriptor systems including model reduction based on balanced truncation. Two projection methods are proposed for calculating low-rank approximate solutions. One is based on the usual Krylov subspace, while the other is based on the union of two different Krylov subspaces. The former is the Krylov subspace method and the latter is the extended Krylov subspace method. For these two methods, exact expressions for the norms of residuals are derived and results on finite termination are presented. Numerical experiments in this paper show the effectiveness of the proposed methods.
Keywords: Projected generalized Lyapunov equation, Projection method, Krylov subspace, Alternating direction implicit method, Matrix pencil, C-stable
Title of the Paper: The Wiener Index for Weighted Trees
Authors: Yajing Wang, Yumei Hu
Abstract: The Wiener index of a graph is the sum of the distances between all pairs of vertices. In fact, many mathematicians have study the property of the sum of the distances for many years. Then later, we found that these problems have a pivotal position in studying physical properties and chemical properties of chemical molecules and many other fields. Fruitful results have been achieved on theWiener index in recent years. Most of the research focus on the extreme values and the corresponding graphs for the non-weighted simple graphs. In this paper, we consider the edge-weighted graphs. Firstly, we give the exact definition of the distances in edge-weighted graphs. Secondly, we get a useful variant formula of theWiener index. Then, we take our attention on edge-weighted trees of order n. We get the minimum, the second minimum, the third minimum, the maximum, the second maximum values of the Wiener index, and characterize the corresponding extremal trees.
Keywords: Weighted graph; Tree; Wiener index; Minimum value; Maximum value; Bound
Title of the Paper: A General Iterative Algorithm for System of Equilibrium Problems and Infinitely many Strict Pseudo-Contractions
Authors: Peichao Duan, Jing Zhao
Abstract: In this paper, an explicit iterative scheme is proposed for finding a common element of the set of fixed point of infinitely many strict pseudo-contractive mappings and the set of solutions of system of equilibrium prob- lems by the general iterative method. In the setting of real Hilbert spaces, strong convergence theorem is proved. Our results improve and extend the corresponding results reported by many others.
Keywords: Strict pseudo-contraction; System of equilibrium problems; Fixed point; Strong convergence; General iterative algorithm
Title of the Paper: On Generalized Preconditioned Hermitian and Skew-Hermitian Splitting Methods for Saddle Point Problems
Authors: Chunping Pan
Abstract: In this paper, we study the iterative algorithms for saddle point problems(SPP). Bai, Golub and Pan recently studied a class of preconditioned Hermitian and skew-Hermitian splitting methods(PHSS). By further accelerating it with another parameters, using the Hermitian/skew-Hermitian splitting iteration technique we present the generalized preconditioned Hermitian and skew-Hermitian splitting methods with four parameters(4- GPHSS). Under some suitable conditions, we give the convergence results. Numerical examples further confirm the correctness of the theory and the effectiveness of the method.
Keywords: Saddle point problems, iterative method, Hermitian and skew-Hermitian splitting method, preconditioned Hermitian and skew-Hermitian splitting method, SOR-like method



